こんにちは。福田泰裕です。
テストが返却されると、教師も生徒も平均点をとても気にします。

今回のテストは平均点が61点でした!

私は65点!
平均点より上で嬉しい!
しかし「平均点が61点」というだけでは、集団全体がどのように得点したのか分かりません。
この記事では、分散を求めてデータの散らばりを知る方法をご紹介します。
最後まで読んでいただけると嬉しいです。
目次
平均値だけで評価するのは危険
まず知っておいていただきたいのは、平均値だけで評価するのは危険だということです。
ある20点満点のテストを2つのクラスで実施して、平均点が次のように同じになりました。

これを見て、

1組と2組は同じくらいよく頑張ったね!
と判断して良いのでしょうか?
1組と2組は平均点が同じ11.0点でも、それぞれの生徒の得点は…👇
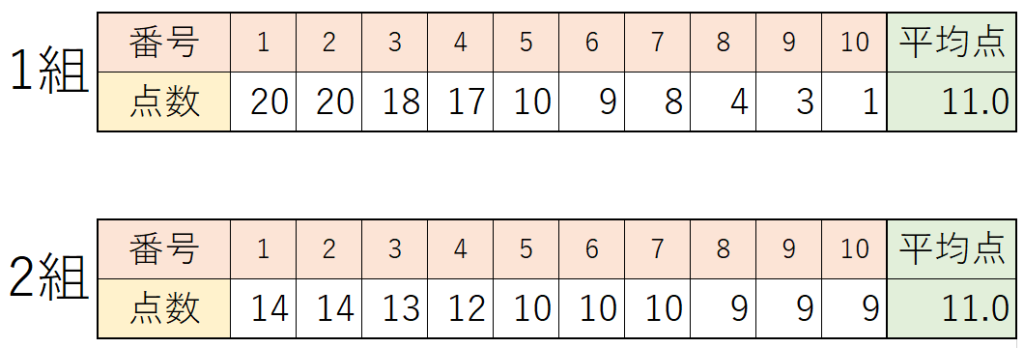
こうなっているかもしれません。
平均点は同じ11.0点でも、2つのクラスの得点状況は全然違いますね。
この結果を見ると、1組と2組に「同じように頑張ったね」とは言えないはずです。
平均値は集団の得点状況を知るために最もよく知られた代表値ですが、平均値だけでは得点の分布を知ることができません。
平均値の問題点についてはこちらの記事で扱っているので、読んでみてください👇
データの散らばり具合を数値化する『分散』
上の1組と2組では、明らかに1組の方が散らばりが大きく、2組の方が散らばりが小さいと言えるでしょう。
それでは、次の2つのクラスはどうでしょう?👇
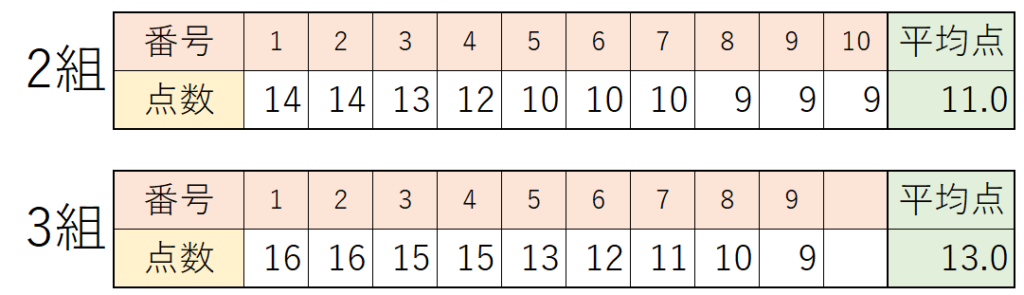
この2つのクラスは平均点が異なりますが、一見同じような得点状況に見えます。
一体どちらのクラスが「より散らばっている」と言えるでしょうか?

2組は最低点が3人もいるから、2組の方が散らばっている!

3組も最高点が3人いるから、散らばりは同じくらい?
このように、人間の直感ほど信用できないものはありません。
データの散らばり具合を数値化していきましょう。
分散を求める手順①:それぞれのデータの偏差を求める
偏差とは、平均値との差です。
例えば平均点70点のテストで75点を取れば、偏差は「+5点」となります。
先ほどのテストの結果からそれぞれのデータの偏差を求めると、次のようになります👇
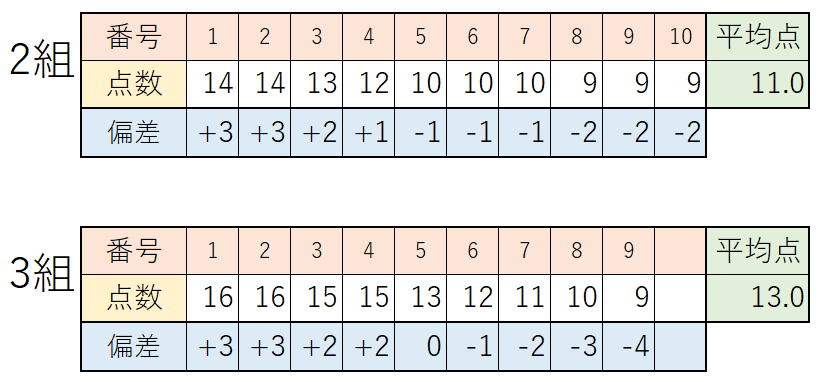
ここで気付く方もいるかもしれませんが、この偏差こそがデータの散らばりです。
平均値から離れた値ほど偏差が大きくなるので、偏差が大きいほどデータが散らばっているということです。
しかし、ここで問題点があります。
「偏差を比べればいい」と思って偏差を合計すると…👇
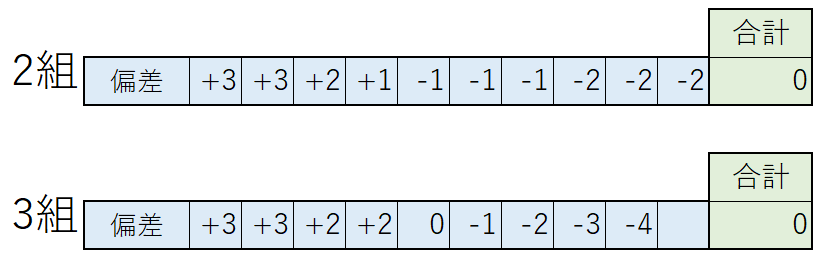
どちらも合計は「0」になってしまいます…。
しかし、これは当たり前のことです。
なぜなら、この偏差の合計を0にする値が平均値だからです。
「どういうこと?」という方は、こちらの記事をご覧ください👇
偏差をそのまま合計しても、散らばりを比較することはできませんでした。
分散を求める手順②:偏差の2乗の平均を求める
偏差の合計が0になるのは、偏差にはプラスとマイナスがあるからです。
それなら、全部プラスにしてしまえば良いじゃないですか?
そういうことで、それぞれのデータの偏差を2乗してみましょう👇
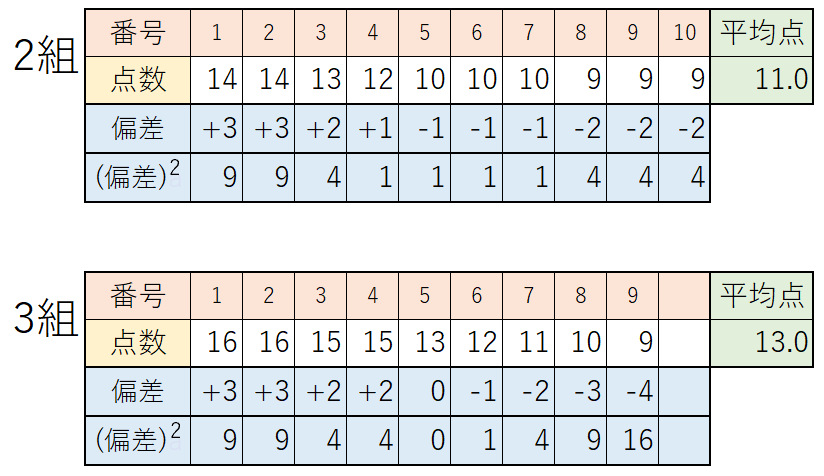
これで、すべての値がプラスになりました。
この偏差の2乗を合計すると…👇
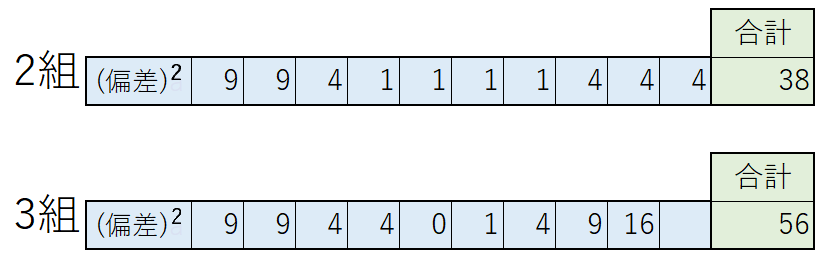
こうなりました。
更に、2つのクラスは人数が違うので、この合計値を単純に比較することはできません。
この合計を人数で割って、平均を求めると…👇
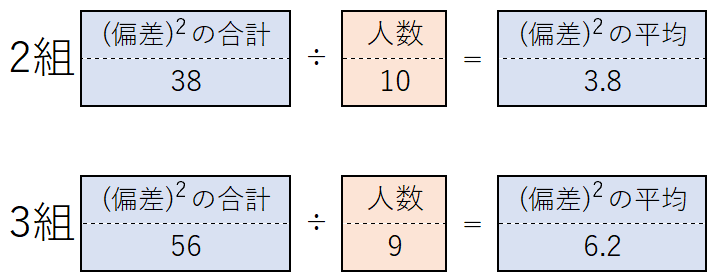
偏差の2乗の平均は、2組が3.8、3組が6.2となりました。
この偏差の2乗の平均が、データの散らばり具合を数値化した『分散』という指標です。
平均値との散らばりの2乗を平均した値です。
3組の方が分散の値が大きいので、「2組より3組の方が散らばりが大きい」と言えるのです。
分散を求める公式
ここまでの話をまとめると、分散とは「偏差の2乗の平均」です。
平均点が \(\bar{x}\) のテストを \(n\) 人が受験したとき、点数が \(x_i\) の生徒の偏差は
$$ x_i – \bar{x} $$
となります。
このまま合計すると0になってしまうので、2乗します👇
$$(x_i – \bar{x})^2$$
これを \(i=1,2,3,\cdots , n\) としながら合計すれば良いので、
$$\sum_{i=1}^{n} (x_i – \bar{x})^2 $$
あとはこの合計を人数 \(n\) で割ると平均になるので…👇
$$\frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2 $$
分散を求める公式が完成します。
\(n\) 個のデータ \(x_1 , x_2 , x_3 , \cdots , x_n\) の平均値を \(\bar{x}\) とすると、分散は
$$\frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2$$
分散の求め方は、「偏差の2乗の平均」で覚えると良いでしょう。
まとめ:分散を求めて散らばりを数値化し、別の集団と比較しよう
いかがでしたでしょうか。
分散を求めることで、データの散らばりを数値化することができます。
これによって、同じ平均点でもどれくらい平均点から散らばっているのかを知ることができます。
例えば、1回目のテストの分散が10、2回目のテストの分散が25だった場合、2回目のテストの方が散らばりが大きくなっていることが分かります。
授業を理解できている生徒と理解できていない生徒の差が大きくなっているということを意味するのかもしれません。
また、同じテストでも1組の分散が15、2組の分散が30だった場合、2組の方が学力に開きがあるということが分かります。
今後の授業を考えるとき、別の手立てを考えなければならないかもしれません。
このように、分散を求めることで平均点だけでは見えてこなかったことも分かるようになるかもしれません。
テストの分析に、ぜひ使ってみてください!
最後まで読んでいただき、ありがとうございました!
質問やご意見、ご感想などがあればコメント欄にお願いします👇





コメント