こんにちは。福田泰裕です。
2020年4月、「ABC予想が証明された!」というニュースが報道されました。
しかし多くの人にとって、

ABC予想って何?
という反応だったと思います。
今回は、このABC予想とはどういうものなのか、またそれが何に役に立つのかについて、できるだけ分かりやすく解説していきます。
最後まで読んでいただけると嬉しいです。
目次
ABC予想とは?
ABC予想は1985年にジョゼフ・オステルレとデイヴィッド・マッサーという2人の数学者によって提起された数論の予想です。
予想なので、「成り立つ気がするけど、証明していない」というものです。
根基(radical)の定義
ABC予想を説明する前に、根基(radical)のお話をします。
【根基(radical)】
自然数 \(n\) に対して、\(n\) と互いに異なる素因数の積を \(n\) の根基(radical) と呼び、
$$\mathrm{rad} \ n$$
と表す。
根基とは、互いに異なる素因数の積です。
言葉だけではよく分からないので、例を示します👇
【根基の例】
- \(\mathrm{rad}(40) =\mathrm{rad}(2^3 \cdot 5) = 2 \cdot 5 = 10\)
- \(\mathrm{rad}(525)=\mathrm{rad}(3 \cdot 5^2 \cdot 7) = 3\cdot 5 \cdot 7 = 105\)
- \(\mathrm{rad}(16)=\mathrm{rad}(2^4)=2\)
- \(\mathrm{rad}(7)=7\)
分かりましたか?
根基とは、「素因数分解をして、指数(右上の小さい数)を取り除いたもの」の積のことです。
一般に、素数 \(p\) に対しては $$\mathrm{rad}\ p=p$$ です。
また、$$\mathrm{rad}(abc) \leq \mathrm{rad}(a) \cdot \mathrm{rad}(b) \cdot \mathrm{rad}(c)$$も成り立ちます。
(\(a,b,c\) のそれぞれの素因数がすべて異なる場合、等号成立。)
この根基を理解できたら、次に進んでください。
弱いABC予想とは?
それでは、ABC予想がどういうものなのか説明します。
【弱いABC予想】
任意の正の数 \(\epsilon\) に対して、\(a+b+c\) を満たす互いに素な自然数の組 \((a,b,c)\) のうち、
$$c>\mathrm{rad}(abc)^{1+\epsilon} $$
を満たすものは高々有限個しか存在しない。
これがABC予想なのですが、ちょっと意味が分かりませんね。
もう少し分かりやすく解説します。
ε = 0 だと、自然数の組は無限に存在する
ABC予想では \(\epsilon >0 \) ですが、まずは \(\epsilon=0\) で考えてみましょう。
互いに素な自然数の組 \((a,b,c)\) を、\(a+b=c\) を満たすように選び、大小を比較してみます。
- 例① \((a,b,c) = (1,2,3)\) のとき、
\(\mathrm{rad}(1 \cdot 2 \cdot 3) = 6\) より、\(3<\mathrm{rad}(1 \cdot 2 \cdot 3)\)
- 例② \((a,b,c) = (2,3,5)\) のとき、
\(\mathrm{rad}(2 \cdot 3 \cdot 5) = 30\) より、\(5<\mathrm{rad}(2 \cdot 3 \cdot 5)\)
- 例③ \((a,b,c) = (5,9,14)\) のとき、
\(\mathrm{rad}(5 \cdot 9 \cdot 14) = \mathrm{rad}(2 \cdot 3^2 \cdot 5 \cdot 7)=2\cdot 3 \cdot 5 \cdot 7= 210\) より、\(14<\mathrm{rad}(5 \cdot 9 \cdot 14)\)
うーん、適当に選ぶと右辺の方が大きくなりそうです。
右辺が小さくなるように工夫してみましょう。
右辺を小さくするためには、素因数分解で指数部分を大きくすれば良さそうです。
- 例④ \((a.b,c)=(1,8,9)\) のとき、
\(\mathrm{rad}(1 \cdot 8 \cdot 9) =\mathrm{rad}(2^3 \cdot 3^2) = 2\cdot 3 =6\) より、\(9 > \mathrm{rad}(1\cdot 8 \cdot 9)\)
- 例⑤ \((a.b,c)=(1,80,81)\) のとき、
\(\mathrm{rad}(1 \cdot 80 \cdot 81) =\mathrm{rad}(2^4 \cdot 3^4 \cdot 5 ) = 2\cdot 3 \cdot 5=30\) より、\(81 > \mathrm{rad}(1\cdot 80 \cdot 81)\)
このように、指数部分が大きくなるように工夫して \((a,b,c)\)を選べば、左辺の方が大きくなりそうです。
実は、\(\epsilon = 0\) のとき、左辺の方が大きくなるような自然数の組 \((a,b,c)\) は無限にあります。
$$(a,b,c)=(1,3^{2^n}-1,3^{2^n})$$とすると、すべての自然数 \(n\) において左辺の方が大きくなります。
【 \((a,b,c)=(1,3^{2^n}-1,3^{2^n}\) とすると、すべての自然数 \(n\) において左辺が大きくなることの証明】
\(a=1,\ b=3^{2^n}-1,\ c=3^{2^n}\) のとき、
\(\mathrm(a)=1,\mathrm{rad}(c)=3\) である。
また、\(3^{2^n} = 9^{2^{n -1}} \) より、\(3^{2^n}\) は \(9\) で割り切れる。
よって、\(3^{2^n} \equiv 1 \pmod 8\) なので、
\(b=3^{2^n}-1 \equiv 1-1=0 \pmod 8\)
となり、\(b\) は \(8=2^3\) で割り切れる。
つまり、自然数 \(\displaystyle M = \frac{b}{8}\) を用いて、\(b=2^3 \cdot M\) と表すことができるので、
\(\mathrm{rad}\ b = \mathrm{rad}(2^3 \cdot M)\)
\(\displaystyle \leq 2M = 2 \cdot \frac{b}{8} =\frac{b}{4}\)
( \(M\) が2の倍数でないとき、等号成立。)
よって、
\(\displaystyle \mathrm{rad}(abc) \leq \mathrm{rad}(a) \cdot \mathrm{rad}(b) \cdot \mathrm{rad}(c)\)
\(\displaystyle \leq 1 \cdot \frac{b}{4} \cdot 3=\frac{3}{4}b <c\)
ゆえに、\(c>\mathrm{rad}(abc)\) である。
この式で、\(n=1\) としたのが例④、\(n=2\) としたのが例⑤です。
ε > 0 として、右辺を少し大きくする
上で述べたように、\(\epsilon=0 \) のときは左辺の方が大きい自然数の組 \((a,b,c)\) は無限に存在しました。
そこで右辺を \(1+\epsilon\) 乗…つまり少し大きくして、自然数の組 \((a,b,c)\) が無限に選べないようにしたいと考えました。
例えば \(\epsilon=1\) とすると、右辺を \(1+1=2\) 乗することになります。
\(\epsilon=0\) の状態では、
例④は \((a,b,c)=(1,8,9)\) で、\(9>6)\)。
例⑤は \((a,b,c)=(1,80,81)\) で、\(81>30)\)
と、左辺が勝っていました。
でも右辺だけ2乗すると、
例④は、\(9<36\)、
例⑤は、\(81<900\)
と、右辺が勝ってしまいます。
そこで \(\epsilon\) を小さくして、右辺を \(1+\epsilon\) 乗します。
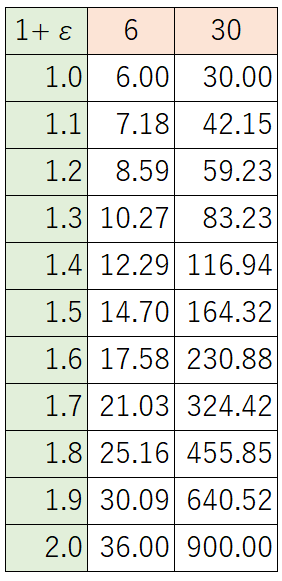
どちらも、1.3乗すると右辺の方が大きくなってしまうようです。
しかし逆に言えば、1.2乗までは左辺の方が大きいようです。
\(\epsilon\) が小さいうちはほとんど変化がないので、左辺の方が大きいままなのです。
今回のABC予想の \(\epsilon\) は任意の正の数なので、極限まで小さくすることができます。
例えば \(\epsilon = 0.0001\) だと、右辺にほとんど変化がありません‥‥‥が、ほんの少しだけ増えています。
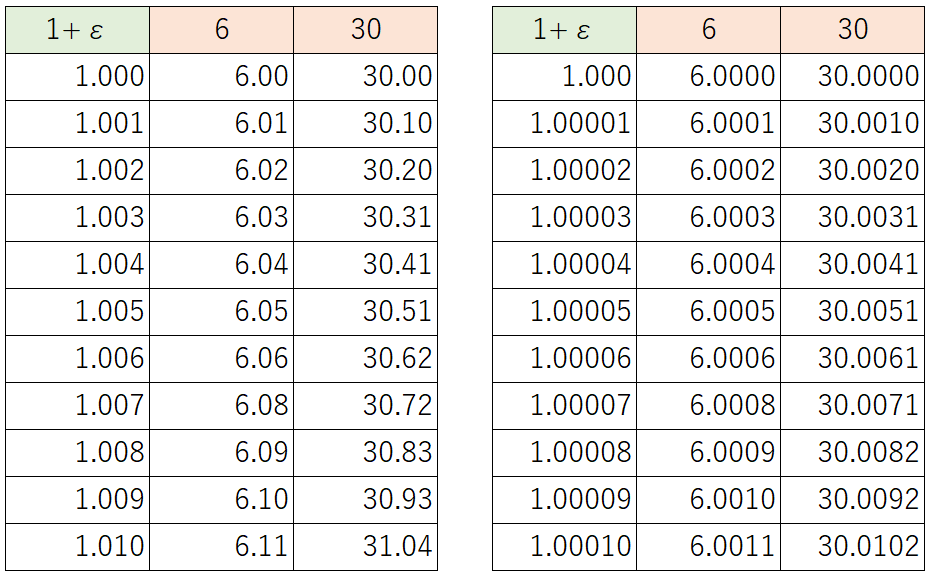
右辺がほんの少しだけ増えたことによって、\(\epsilon=0\) のときは無限にあった自然数の組が、\(\epsilon>0\) だと有限になってしまう(だろう)というのが弱いABC予想です。
強いABC予想とは?
上で示したABC予想は、「弱いABC予想」です。
それに対して「強いABC予想」というものがあります。
弱いABC予想を同値変形して得られる次の式が、強いABC予想です。
【強いABC予想(弱いABC予想と同値)】
任意の正の数 \(\epsilon\) に対して、\(\epsilon\) に依存する数 \(K(\epsilon)>0\) が存在し、\(a+b+c\) を満たす互いに素なすべての自然数の組 \((a,b,c)\) に対して
$$c<\underline{K(\epsilon) \cdot} \mathrm{rad}(abc)^{1+\epsilon} $$
が成り立つ。
弱いABC予想をどうやって同値変形したらこうなるのか、残念ながら筆者には分かりません💦
しかし、かなり言い回しが変わっています。
弱いABC予想は「\(>\) となるのは有限個」だったのが、強いABC予想では「すべて \(<\) が成り立つ」となりました。
右辺に係数 \(K(\epsilon)\) をかけて、すべての場合において右辺が大きくなるようにしようというものです。
先ほどの「無限ではないこと」を証明するのは難しそうですが、こちらは「 \(epsilon\) に対して、係数 \(K(\epsilon)\) をどう取ればよいか」を考えれば良いので、直感的には理解しやすいのかな…と思います。
ABC予想の証明が正しいと分かるまで8年かかった
2012年、京都大学数理解析研究所の望月新一教授が、個人ホームページに「宇宙際タイヒミュラー理論」と題する4篇の論文をアップロードしました。
なんと、補足を含めると600ページにも及ぶ超大作です。
27年間未解決だった問題だったため、世界中から注目されました。
通常の数学の論文というのは、学術雑誌へ投稿され、専門家たちが読んで正しいと判断する “査読” という作業が行われます。
その査読を経て、ようやく認められるのです。
しかしこのABC予想の論文は難しすぎて、誰にも理解できませんでした。
論文に書かれている「宇宙際タイヒミュラー理論」は、望月教授が20年以上かけて構築した独自の理論だったのです。
望月教授によって考えられた用語や定義が多くあり、専門家ですら理解できませんでした。
(ちなみにこのブログの筆者も論文を見てみましたが、当然ながら何一つ理解できませんでした。)
査読をしようにも理解できる人がいないため、望月教授による査読のための勉強会が開かれたらしいです。
そしてアップロードから8年後の2020年4月。
ようやく論文に誤りがないと認められ、世界的に認められることになりました。
ABC予想は整数について述べられている問題ですが、望月教授はこれを楕円曲線について置き換えて、新たな概念を用いて証明を行っています。
「我こそは!」という方は、原文のリンクを置いておくのでご覧ください👇
http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20I.pdf
http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20II.pdf
http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20III.pdf
http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20IV.pdf
まとめ:ABC予想の理屈は単純なのに、証明は難しい
いかがでしたでしょうか。
ABC予想というのは整数に関するものなので、理屈を理解することはそこまで難しいものではありません。
しかし証明するためには整数の枠を飛び越え、27年の歳月がかけられることになりました。
ところで、ABC予想が何の役に立つのか疑問に思われる方も多いと思います。
そういう方のために、このような記事をオススメします👇
最後まで読んでいただき、ありがとうございました。
質問やご意見、ご感想などがあればコメント欄にお願いします👇




コメント
【定理】n≧3のとき、x^n+y^n=z^nは自然数解を持たない。
【証明】x,y,aは有理数とする。
x^n+y^n=z^nを、z=x+rとおくと、x^n+y^n=(x+r)^n…(1)となる。
(1)はr^(n-1){(y/r)^n-1}=an{x^(n-1)+…+r^(n-2)x}(1/a)…(2)となる。
(2)はa=1、r^(n-1)=nのとき、x^n+y^n=(x+n^{1/(n-1)})^n…(3)となる。
(2)はa=1以外、r^(n-1)=anのとき、x^n+y^n=(x+(an)^{1/(n-1)})^n…(4)となる。
(3)はrが無理数なので、成立しない。(3)(4)の解の比は同じなので、(4)も成立しない。
∴n≧3のとき、x^n+y^n=z^nは自然数解を持たない。