 入試問題
入試問題 【共通テスト2024】数学ⅡB 解答と解説
2024年1月14日(日)に実施された、令和6年度(2024年度)共通テストの『数学Ⅱ・B』の解答と解説を掲載しています。解いてみた感想としは、難易度・計算量ともに昨年並みでした。昨年は積分でソメイヨシノの開花予想をさせられたり、数列で複利計算をさせられたりしましたが、今年は普通の数学をさせてたのが嬉しいです。
 入試問題
入試問題  入試問題
入試問題 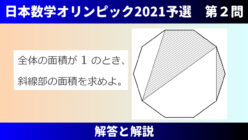 数学オリンピック
数学オリンピック  数学オリンピック
数学オリンピック  入試問題
入試問題  入試問題
入試問題  面白い数学
面白い数学  面白い数学
面白い数学  面白い数学
面白い数学