こんにちは。福田泰裕です。
この記事では、2021年日本数学オリンピック(JMO)第1問の問題を解説していきます。
最後まで読んでいただけると嬉しいです!
【日本数学オリンピック(JMO)予選2021第1問】問題
互いに素な2つの整数 \(m,n\) が \(m + n = 90\) をみたすとき、積 \(mn\) としてありうる最大の値を求めよ。
【日本数学オリンピック(JMO)予選2021第1問】考察
【考察①】「互いに素」でなければ、どうなる?
まず、問題を単純にして考えてみましょう。
問題文前半の「互いに素」という条件を取り除き、
2つの整数 \(m,n\) が \(m + n = 90\) をみたすとき、積 \(mn\) としてありうる最大の値を求めよ。
として、考えてみます。
\(y = mn\) とすると、\(n = 90-m\) より、
\[
\begin{split}
y &= m(90-m) \\
&= -m^2+90m \\
&= -(m-45)^2+2025 \\
\end{split}
\]
よって、\(m = n = 45\) のとき、積 \(mn\) の最大値は \(2025\)
これなら、数学Ⅰの教科書に出そうなレベルの問題ですね。
ただ、今回の問題は「互いに素な2つの整数 \(m,n\)」なので、もう少し考察を進めていきましょう。
【考察②】\(m,n\) の見つけ方
\(y = -(m-45)^2+2025\)
のグラフを描くと、下のようになります。
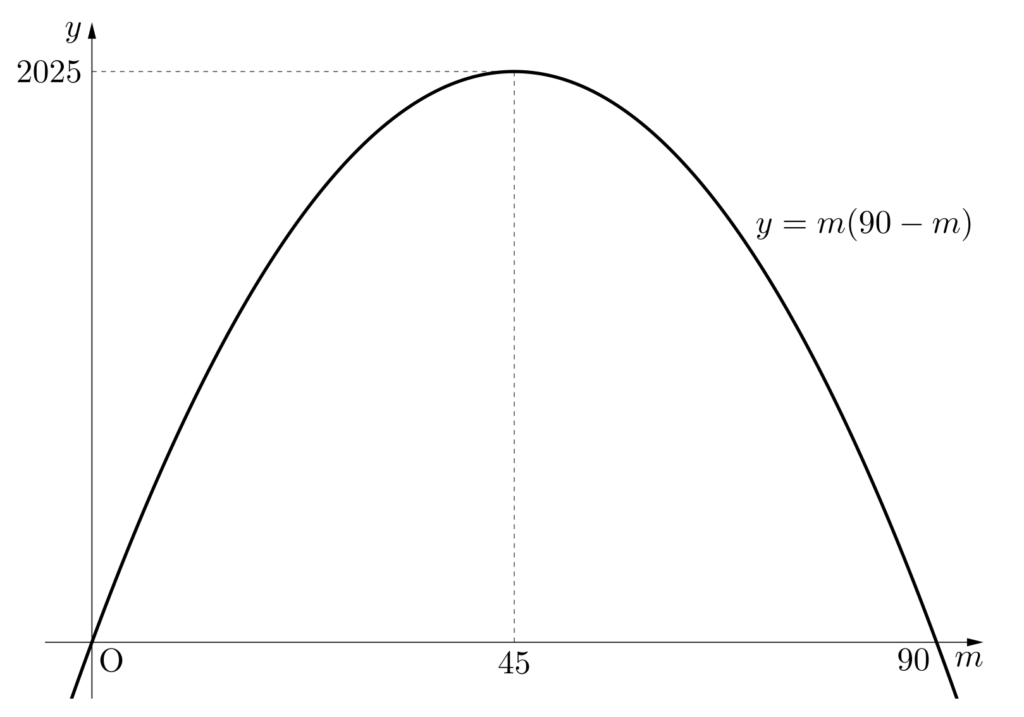
これから、「 \(m,n\) が \(45\) に近いほど、積 \(mn\) が大きくなる」ということが分かります。
ここに「互いに素」という条件が加わるので、
『①互いに素な \(m,n\)』かつ『② \(m+n = 90\) を満たす』
という大前提を満たす\(m,n\)のうち、『できるだけ \(45\) に近くなる』ような2つの整数を見つけましょう。
【考察③】実際に \(m,n\) を見つける
上の3つの条件を考慮して、\(m,n\) を考えてみましょう。
\(m,n\) は対等な関係なので、今回は \(m<n\) として考えます。
『 \(m,n\) が互いに素』かつ『 \(m+n = 90\) 』を満たすのは、
\( (m,n) = \)(44,46)\(, (43,47), \cdots\cdots \)
であり、\((m,n) = (43,47)\) のときの積 \(mn = 43 \times 47 = 2021\) が最大であると予想できます。
あとは、この積 \(2021\) が最大であることを論理的に示せばよいでしょう。
(実際のJMO予選は答えのみで良いのですが、一応掲載しておきます。)
【日本数学オリンピック(JMO)予選2021第1問】解答
\((m,n) = (43,47)\)
は条件を満たし、このとき \(mn = 43 \times 47 = 2021\) である。
以下、この \(mn = 2021\) が最大であることを示す。
\[\begin{split}
mn &= m(90-n) \\
&= -(m-45)^2+2025 \\
\end{split}\]
であるから、\(|m-45|\) が小さいほど、\(mn\) は大きくなる。
\(|m-n| \leq 1\) を満たすのは
\[(m,n) = (44,46),(45,45),(46,44)\]
だが、これらはすべて \(m,n\) が互いに素であるという条件に反する。
よって、\(|m-n| = 2\) を満たす \((m,n) = (43,47)\) のとき、\(|m-n|\) が最小となるため、積 \(mn\) が最大となる。
ゆえに、求める積 \(mn\) の最大値は \(43 \times 47 = 2021\)
【日本数学オリンピック(JMO)予選2021第1問】まとめ
いかがだったでしょうか。
2021年JMO予選の問題の答えが『2021』という、さっそくユーモアのある問題でした。
この問題は、普通に数学が得意な高校生ならきっと正解できる難易度だと思います。
最後まで読んでいただき、ありがとうございました!
ご意見やご感想、質問などあれば、コメント欄にお願いします👇


コメント