こんにちは。福田泰裕です。
突然ですが、オイラーの多面体定理を知っていますか?
多面体を語る上では避けては通ることのできない重要な定理です。
今回はこのオイラーの多面体定理が成り立つ証明を、丁寧に解説します。
最後まで読んでいただけると嬉しいです。
目次
オイラーの多面体定理とは?

まず、オイラーの多面体定理を紹介します。
【オイラーの多面体定理】
凸多面体(へこみのない多面体)において、頂点の数を \(v\) 、辺の数を \(e\) 、面の数を \(f\) とすると、次の式が成り立つ。
$$v-e+f=2$$
\(v\) ,\(e\) ,\(f\) というのは、頂点(Vertex)、辺(Edge)、面(Face) それぞれの頭文字です。
本当に成り立つのか、例を見ていきましょう。
オイラーの多面体定理の例①:正四面体
まず、最も簡単な正四面体で調べてみましょう。
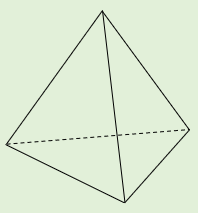
正四面体は、頂点の数 \(v=4\) 、辺の数 \(e=6\) 、面の数 \(f=4\) なので、
\(v-e+f=4-6+4=2\)
確かに、オイラーの多面体定理が成り立ちます。
オイラーの多面体定理の例②:正六面体
次に、正六面体でも調べてみましょう。
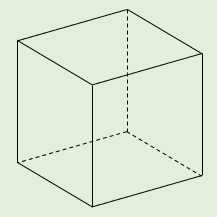
正六面体は、頂点の数 \(v=8\) 、辺の数 \(e=12\) 、面の数 \(f=6\) なので、
\(v-e+f=8-12+6=2\)
確かに、オイラーの多面体定理が成り立ちます。
オイラーの多面体定理の証明
正四面体と正六面体で成り立つのは分かりましたが、この方法を繰り返していてもオイラーの多面体定理の証明にはなりません。
凸多面体は無限にあるので、この方法では証明が終わることはないのです。
オイラーの多面体定理で重要なのは、頂点の数、辺の数、面の数の3つの要素です。
辺の長さ、面の大きさなどは関係ありません。
このことを踏まえて、証明を見ていきましょう。
手順①:多面体を地面に押し広げる
まず、多面体を地面に置きます。
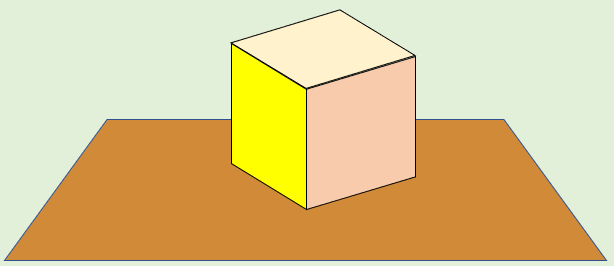
そして、面を1つ取り除きます。
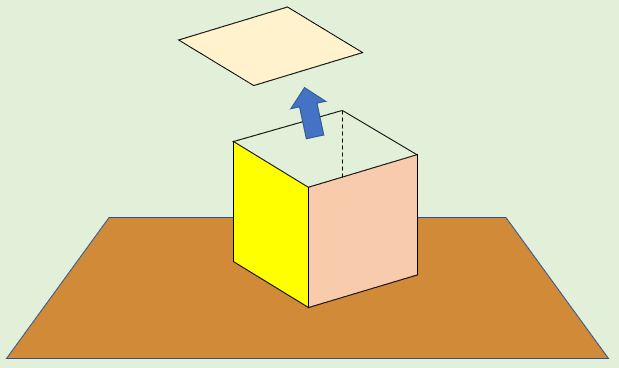
そこに手を突っ込み、すべての辺と頂点が地面につくように内側から押し広げていきます。
このとき、辺は自由に伸び縮みする魔法の棒だと思ってください。
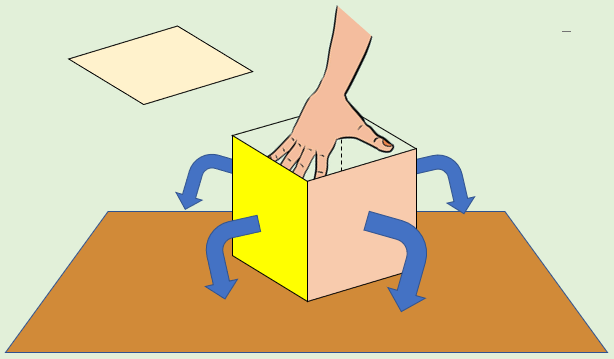
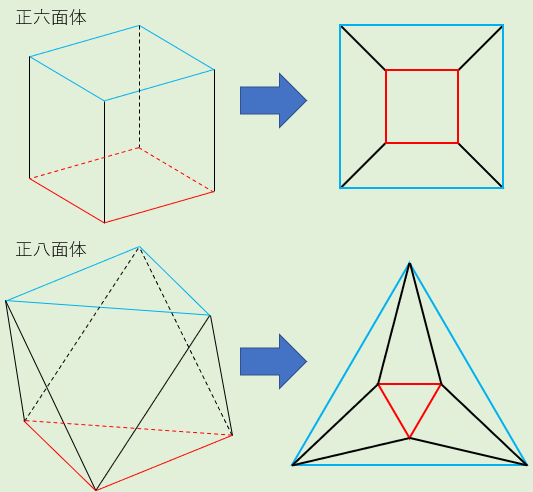
すると、正六面体や正八面体の場合は次のようになります👇
(それぞれ赤い辺で囲まれた面が地面にあり、青い辺で囲われた面から腕を入れて押し広げています。)
手順②:辺を加えて、すべての面を三角形にする
正四面体や正八面体のように、すべての面が三角形ならばそれで良いのですが、正六面体のように四角形があったり正十二面体のように五角形がある場合は、適当に辺を加えてすべての面を三角形にします。
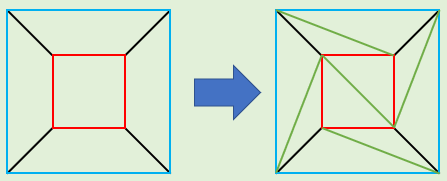
辺を1本加えると、1つの面が2つに分割されます。
頂点の数は変わりません。
よって、\(v\) はそのまま、\(e\) は \(+1\) 、\(f\) も \(+1\) されるので、
\(v-e+f\) の値に変化はありません。
手順③:三角形を外側から取り除いていく
ここまでの手順で、すべての多面体が地面に押し広げられ、すべての面が三角形の形になっている状態です。
次は、その図形の三角形を外側から取り除いでいきます。
まず、外側と1辺を共有する三角形を取り除く場合を考えます。
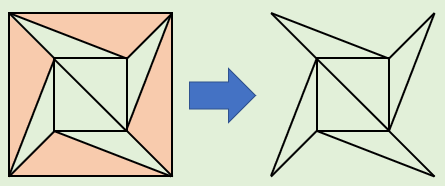
このとき、頂点の数 \(v\) はそのまま、辺の数 \(e\) は \(-1\) 、面の数 \(f\)は \(-1\) されます。
よって、\(v-e+f\) の値に変化はありません。
次に、外側と2辺を共有する三角形を取り除く場合を考えます。
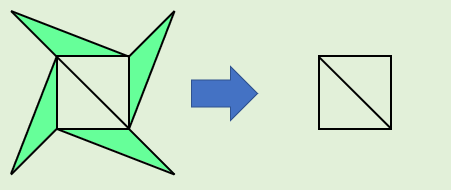
このとき、頂点の数 \(v\) は \(-1\)、辺の数 \(e\) は \(-2\) 、面の数 \(f\)は \(-1\) されます。
この場合も、\(v-e+f\) の値に変化はありません。
つまりどのような状況でも、外側から三角形を取り除くとき、\(v-e+f\) の値に変化はないということです。
手順④:最後に残る1つの三角形で考える
手順③を繰り返していくと、\(v-e+f\) の値に変化がないまま三角形がどんどん取り除かれていき、最終的には三角形が1つだけ残ります。

1つの三角形を調べてみると、頂点の数 \(v\) は \(3\)、辺の数 \(e\) は \(3\) 、面の数 \(f\)は \(1\) なので、
\(v-e+f=3-3+1=1\) となります。
逆にたどっていくと、手順②と手順③では \(v-e+f\) の値に変化はないので…👇
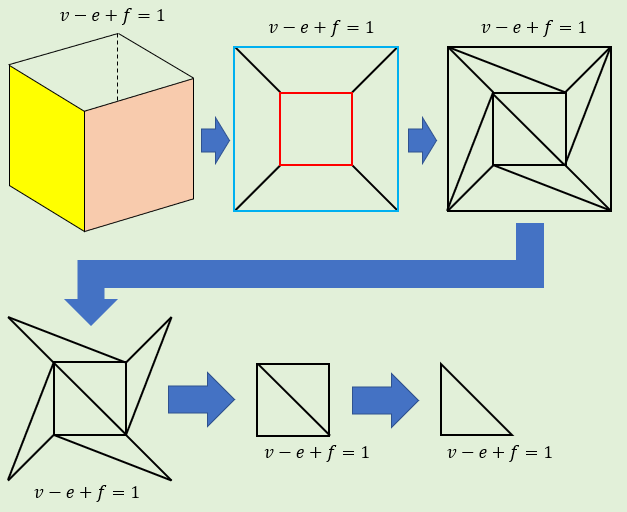
これらすべての図形は \(v-e+f=1\) となります。
そして、忘れていはいけません。
最初に取り除いた面を使ってこの多面体に蓋をすると…👇
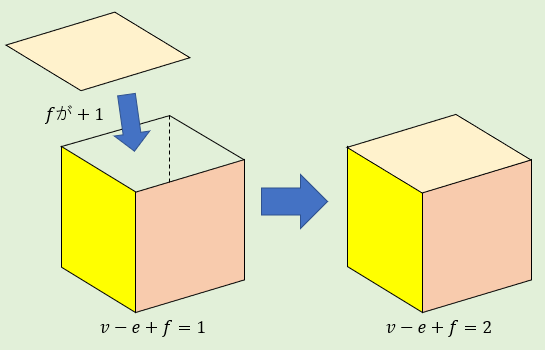
頂点の数 \(v\) はそのまま、辺の数 \(e\) はそのまま、面の数 \(f\)は \(+1\) されるので、
\(v-e+f=2\) となります。
これで証明は終わりです。
まとめ:オイラーの多面体定理は証明も含めて美しい
いかがでしたでしょうか。
このオイラーの定理は高校数学で学習します。
しかし、大学入試で出題されることはほとんどないため、影の薄い定理です。
多くの受験生にとって、覚える必要のない定理として認識されているでしょう。
しかし、高校数学で学習する定理の中でも、この定理の証明方法は異彩を放っています。
ほとんどの定理が計算や図形の性質を利用して導かれるのに対して、この定理はまったく違うアプローチをしています。
ぜひこのオイラーの多面体定理は、\(v-e+f=2\) という式だけでなく、証明方法まで併せて知ってほしいと思います。
例え理解できなくても、こういったアプローチがあることを知るだけでも、数学の世界が広がるのではないでしょうか。
最後まで読んでいただき、ありがとうございました!
質問やご意見、ご感想などがあればコメント欄にお願いします👇



コメント