【面白い確率】ウイルス検査で陽性だったとき、実際に感染している確率

こんにちは。福田泰裕です。

インフルエンザや百日咳などの感染症にかかると学校への出席が禁止されています。
また、新型コロナウイルスなど未知の感染症が流行してしまうと世界中が大混乱になります。

病院でウイルス検査をして感染しているのかを確かめるのですが、結果が陽性だったとき本当に感染しているといえるのでしょうか？

今回は、ウイルス検査で陽性だったとき、実際に感染している確率について考えていきます。

最後まで読んでいただけると嬉しいです。

例題：感染率0.01%、検査精度95%の場合

まず、計算方法を確認するための例題です。

まず、直感で予想してみましょう。
次のうち、正解はどれだと思いますか？

A…約95%
B…約60%
C…約35%
D…約2%
E…約0.2%

予想できましたか？
それでは、解説していきます。

確率の計算方法

感染する確率は \(\displaystyle 0.01\% = \frac{1}{10000}\) で、検査の精度は \(\displaystyle 95\% = \frac{19}{20}\) です。

そして、「検査を受けて結果が陽性である」というのは、
① 実際に感染していて、結果が正しい場合
② 実際は感染しておらず、結果が誤りの場合
の 2 種類あります。

①「実際に感染していて、結果が正しい場合」は、
感染する確率が \(\displaystyle \frac{1}{10000}\) 、検査結果が正しい確率が \(\displaystyle \frac{19}{20}\) なので、①の確率は$$\frac{1}{10000} \times \frac{19}{20} = \frac{19}{200000}$$となります。

②「実際に感染しておらず、結果が誤りの場合」は、
感染していない確率が \(\displaystyle \frac{9999}{10000}\) 、検査結果が誤りである確率が \(\displaystyle \frac{1}{20}\) なので、①の確率は$$\frac{9999}{10000} \times \frac{1}{20} = \frac{9999}{200000}$$となります。

この①と②は同時には起こらない（互いに排反）なので、「検査を受けて結果が陽性である確率」は「①+②」で、$$\frac{19}{200000} + \frac{9999}{200000} = \frac{10018}{200000}$$です。

このうち、実際に感染しているのは①なので、計算は「①/(①+②)」となり、
$$\frac{\frac{19}{200000}}{\frac{10018}{200000}} =\frac{19}{10018}$$
$$=‭0.001896586‥‥‥ = 約0.2\%‬$$となります。

よって、正解は E…約0.2% でした！
精度95%なのに、実際に感染している確率は0.2%とは…意外な結果にビックリですね！

確率の計算方法（人数に置き換える分かりやすい方法）

上の計算は確率の分数計算ばかりで、いまいちピンと来なかったと思います。
そこで、人数に置き換える分かりやすい計算方法をご紹介します。

確率では全体を「1」として計算しますが、今回は全体を「200,000人」として計算していきましょう。

まず、感染する確率は0.01%なので、
感染している人は \(200,000人 \times 0.01\% = 20人\)、
感染していない人は \(200,000人 – 20人 = 199,980人\) です。

感染している20人のうち、
検査結果が正しく「陽性」となるのは \( 20人 \times 95\% = 19人\)、
検査結果が誤って「陰性」となるのは \( 20人 – 19人 = 1人\)です。

感染していない 199,980人のうち、
検査結果が誤って「陽性」となるのは \( 199,980人 \times 5\% = 9999人\)、
検査結果が誤って「陽性」となるのは \( 199,980人 – 9999人 = 189,981人\)です。

つまり、陽性と判断されるのは\( 19人 + 9,999人 = 10,018人\)です。
そのうち、本当に感染しているのは19人なので、確率は$$\frac{19}{10018} = 0.001896586‥‥‥ = 約0.2\%‬$$となります。

確率の問題は、分数から離れて整数にして考えると分かりやすいですね。

陽性反応のとき、本当に感染している確率の一般化

それでは計算方法が分かったところで、この問題を一般化しておきましょう。

このように、文字でおいた状態で計算していきましょう。

先ほどと同じように考えると、
感染している確率は \(P_1\) なので、感染していない確率は \(1-P_1\) です。

そして、「検査を受けて結果が陽性である」というのは、
① 実際に感染していて、結果が正しい場合
② 実際は感染しておらず、結果が誤りの場合
の 2 種類あります。

①「実際に感染していて、結果が正しい場合」は、
感染する確率が \(P_1\) 、検査結果が正しい確率が \(P_2\) なので、①の確率は$$P_1 P_2$$となります。

②「実際に感染しておらず、結果が誤りの場合」は、
感染していない確率が \(1 – P_1\) 、検査結果が誤りである確率が \(1 – P_2\) なので、①の確率は$$(1-P_1)(1-P_2)$$となります。

この①と②は同時には起こらない（互いに排反）なので、「検査を受けて結果が陽性である確率」は「①+②」で、$$P_1 P_2 + (1 – P_1)(1 – P_2)$$です。

このうち、実際に感染しているのは①なので、計算は「①/(①+②)」となり、$$\frac{P_1 P_2}{P_1 P_2 + (1 – P_1)(1 – P_2)}$$となります。

結果の考察

この計算結果をグラフにして見てみましょう。
$$ z = \frac{P_1 P_2}{P_1 P_2 + (1 – P_1)(1 – P_2)} $$をグラフにすると次の通りです👇

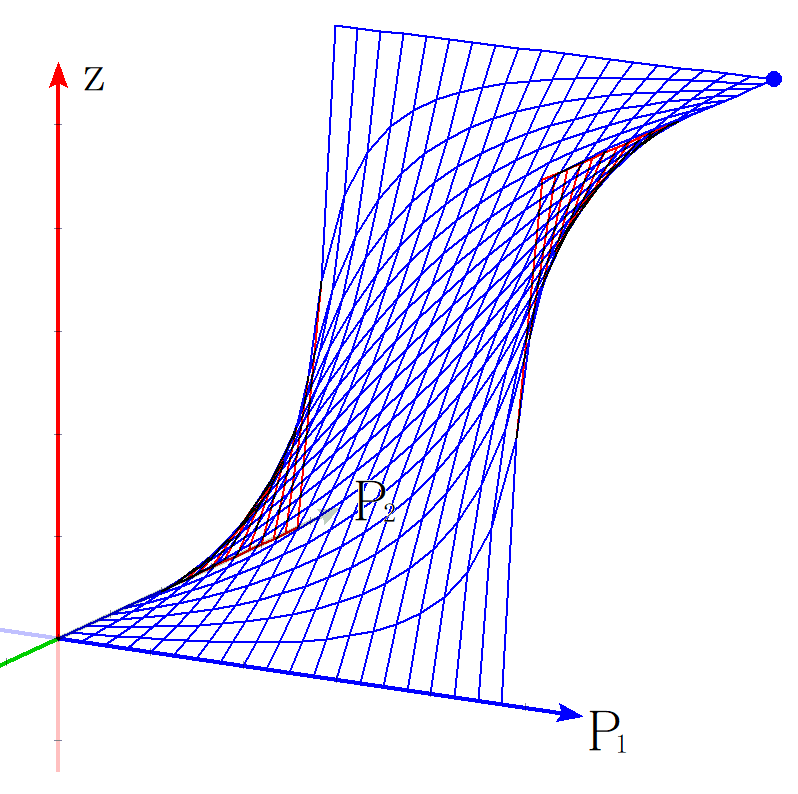
\(P_1\) と \(P_2\) のうち、どちらか一方が 1 ならば必ず \(z = 1\) となり、
どちらか一方が 0 ならば必ず \(z = 0\) となるようです。

検査の精度 \(P_2 = 95\%\) と固定すると、

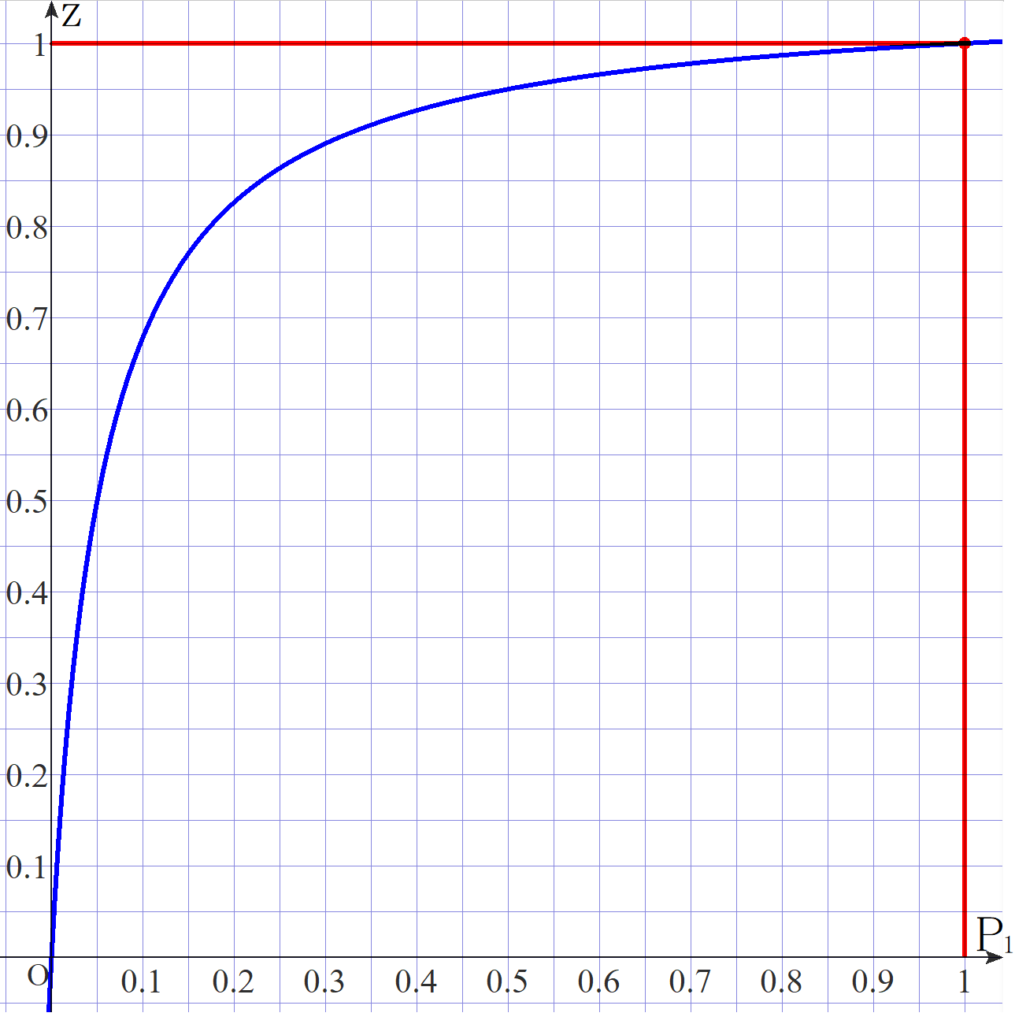
このようなグラフになります。
感染率 \(P_1 = 50\%\) でようやく本来の精度 95% となるのですね。

逆に、感染率を \(P_1 = 0.01\%\) で固定すると、

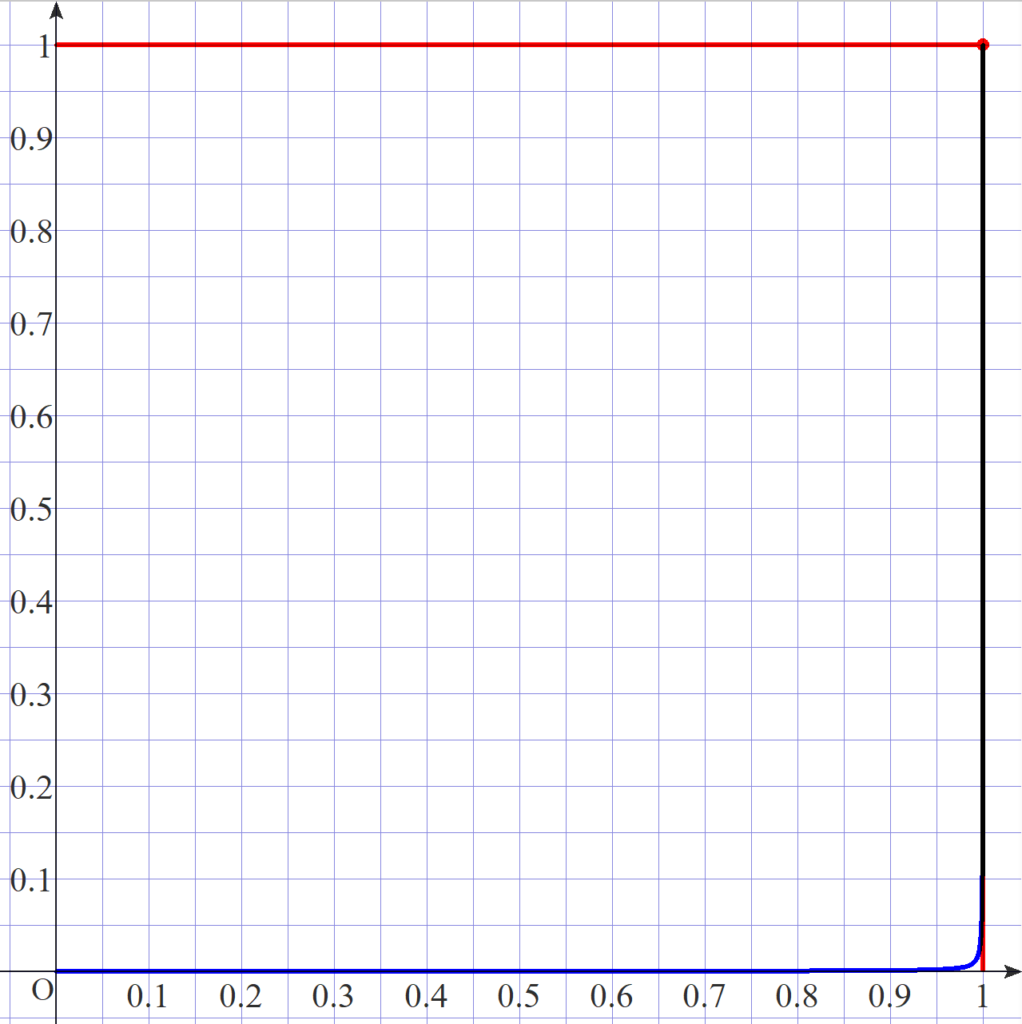
このような悲惨なグラフになります…！
どれだけ精度を高めても、実際に感染している確率はほとんど変化がないようです。
このグラフの最後の方は、次ようになっています。

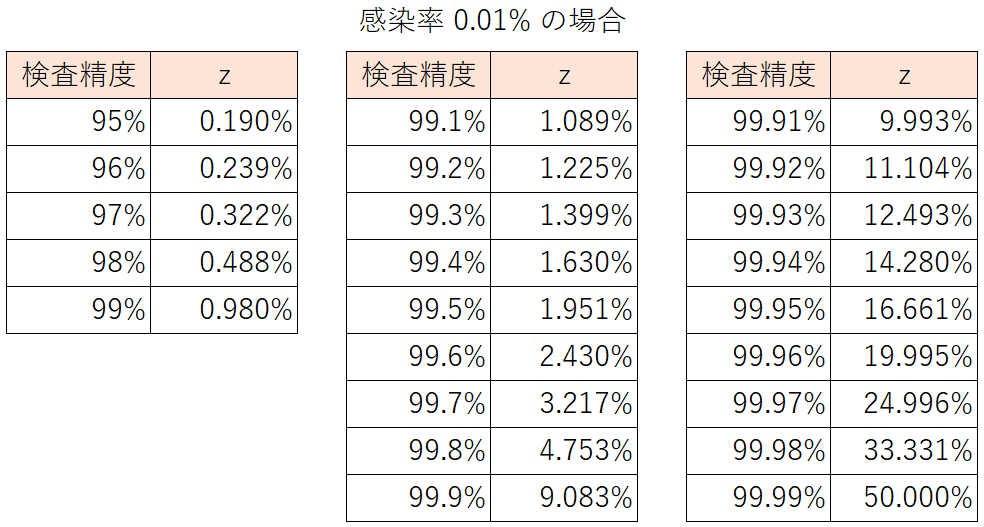
検査の信頼を高めるためには、かなりの精度が要求されるようです…。

まとめ：精度95%でも感染している確率は意外な結果に！

いかがでしたでしょうか。

今回の記事をまとめると、次のようになります。

検査結果が「陽性」なのに、実際に感染している確率は0.2%というのは直感とかなり違う結果になったと思います。
確率の問題は面白いですね！

最後まで読んでいただき、ありがとうございました。

質問やご意見、ご感想などがあればコメント欄にお願いします👇